🌈 Getting to Know Gradient Descent
Before we dive in, let's touch on the basics of Gradient Descent. This is a method we often use to minimize our cost function, or error, in machine learning algorithms. Sounds good, right? But there's a catch - sometimes, it can be a slow process.
This is where the learning rate comes into play. We can speed up convergence by increasing the learning rate, but in some scenarios this might cause the cost function to oscillate due to the shape characteristics of the function itself. If we're not careful, the cost function could even diverge. This means we often have to be patient and wait, even if the learning speed seems sluggish.
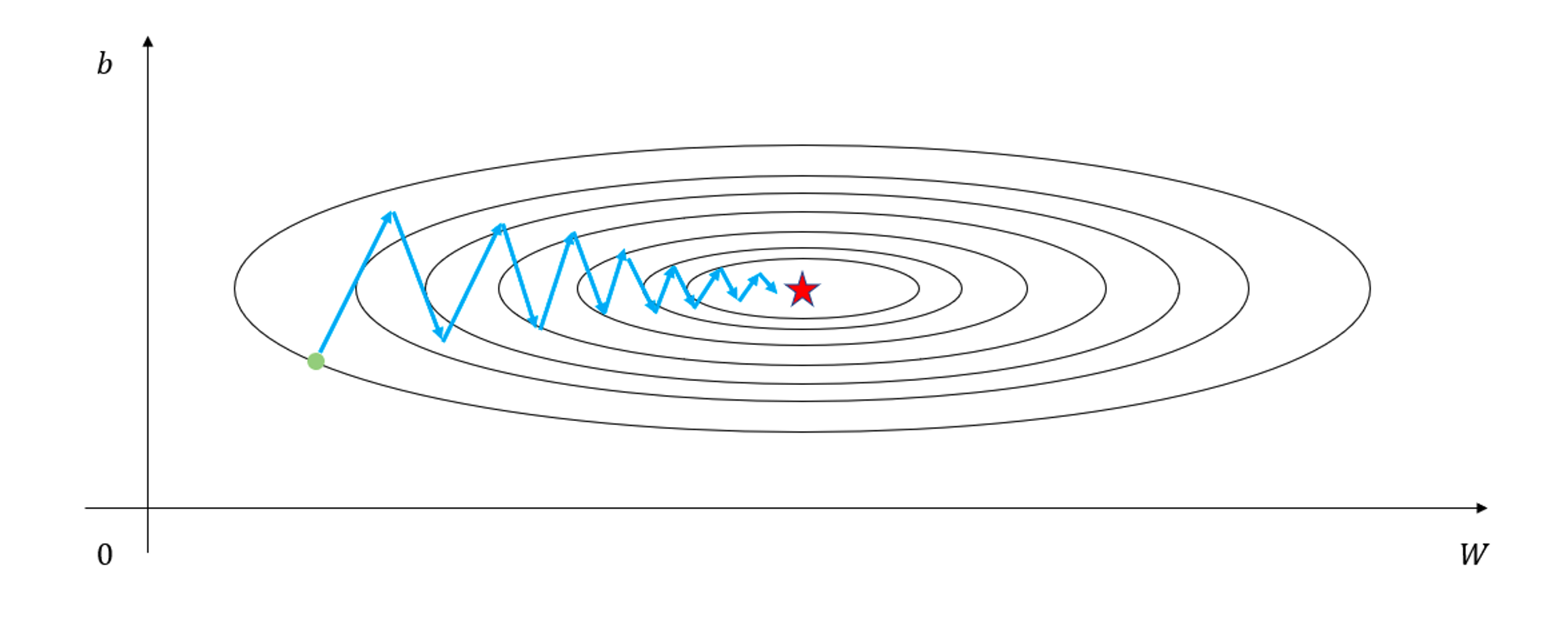
Let's look at Figure 1, where the parameter b oscillates before it eventually converges to the minimum value. This is due to the gradient vector's nature which points in the direction perpendicular to the contour line.

The ideal situation? We want to converge slowly in the vertical direction and quickly in the horizontal direction (check out Figure 2).
🚀Adding Momentum to Gradient Descent
Gradient Descent with Momentum is like an upgrade! It's designed to slow down the updates if the direction keeps changing in every iteration, and to speed up if the direction remains the same.
🎯Momentum Algorithm:
We start with
During the t-th iteration:
- We calculate for the current batch.
- Next, we compute:
- Finally, we update our Weight and Bias as follows:
(where α is the learning rate)
The core of the Momentum algorithm is Equations (1) and (2), but since the form is almost the same, let's solve Equation (1) a little more and think about it.
Equation (1) is a recursively calculated term, which will be as follows if we look at it step by step from iteration 1.
iteration 1
iteration 2
iteration 3
Normalize
normally
As we iterate, we can see that gradients in the b-axis that change up and down will gradually approach zero, while those in the W-axis will continue to speed up. This shows that the momentum algorithm adjusts the learning speed for each parameter appropriately.
🌪️RMSProp: Harnessing the Power of Propagation
RMSProp, although not officially presented in an academic paper, has proven its worth in the machine learning field. It's quite similar to Gradient Descent with Momentum, but uses the size of the gradient to adjust the learning speed for each parameter.
🎯RMSProp Algorithm:
We start with
During the t-th iteration:
- We calculate for the current batch.
- Next, we compute:
- Finally, we update our Weight and Bias as follows:
(where α is the learning rate)
RMSProp adjusts the learning rate for each parameter based on the size of the gradient, thus allowing for efficient learning.
🎯ADAM: The Best of Both Worlds
ADAM (Adaptive Moment Estimation) is like a supercharged method that uses both Gradient Descent with Momentum and RMSProp.
The ADAM algorithm:
We start with
During the t-th iteration:
- We calculate for the current batch.
- Next, we compute:
- Finally, we update our Weight and Bias as follows:
(where α is the learning rate)
The creators of the ADAM algorithm suggest using , and for best results. With ADAM, you're combining the advantages of two powerful algorithms for efficient optimization!